Kalkulator Vektor
Apa itu Vektor?
Vektor adalah besaran yang mempunyai nilai dan arah. Contohnya adalah:
- Perpindahan
- Kecepatan
- Percepatan
- Momentum
- Gaya
Misalnya untuk menyebutkan sebuah besaran vektor adalah “Nisa berlari ke utara dengan kecepatan 5 km/jam“. Biasanya vektor dinyatakan dalam huruf kapital yang tebal seperti A, B, dan Y. Sebuah vektor juga biasanya digambarkan dengan anak panah. Panjang anak panah tersebut menyatakan besar vektor, sedangkan arahnya menyatakan arah vektor.
Apa saja metode untuk menghitung resultan vektor?
Ada beberapa cara yang dapat digunakan untuk menghitung resultan vektor, yaitu metode segitiga, metode jajargenjang, metode poligon, dan metode analisis. Dalam postingan ini, kita akan membahas cara menghitung resultan vektor menggunakan metode analisis. Metode analisis adalah metode yang dapat menghitung resultan vektor untuk dua atau lebih vektor.
Bagaimana cara menghitung resultan vektor menggunakan metode analisis?
Untuk menghitung resultan vektor menggunakan metode analisis, ada beberapa langkah yang harus dilakukan:
- Hitung komponen vektor untuk semua vektor
- Tentukan apakah hasil uraian vektor adalah positif atau negatif
- Hitung resultan vektor pada sumbu x
- Hitung resultan vektor pada sumbu y
- Hitung resultan vektor untuk semua vektor
Contoh soal :
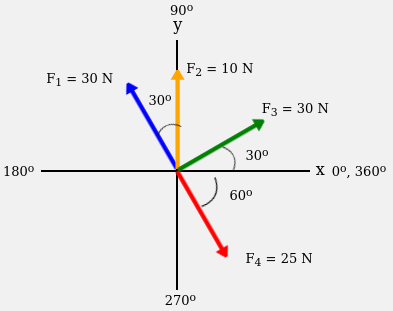
Dalam gambar tersebut, diketahui 4 buah vektor. Untuk mengetahui resultan vektor dari 4 vektor tersebut, langkah pertama yang harus dilakukan adalah menghitung komponen vektor pada sumbu x dan y untuk vektor-vektor tersebut. Komponen vektor adalah proyeksi dari satu vektor menjadi dua komponen yang saling tegak lurus.
Rumus untuk menghitung komponen vektor melibatkan fungsi trigonometri. Perhatikan gambar segitiga AOB dibawah yang besar sudutnya adalah α derajat dan siku-siku di B. Panjang AB dapat dicari dengan fungsi sinus, sedangkan panjang OB dapat dicari dengan panjang cosinus.
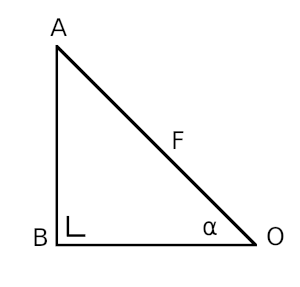
Sehingga rumus untuk menghitung sisi OB dan AB adalah :
| Rumus sisi OB | OB = F × cos α |
|---|---|
| Rumus sisi AB | AB = F × sin α |
Dimana F adalah panjang vektor dan α adalah sudut vektor.
Untuk dapat memahami lebih lanjut, ayo kita coba menghitung komponen vektor untuk contoh soal diatas!
-
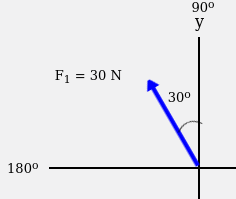
Untuk vektor F1, diketahui memiliki panjang 30 N dan menghadap 30o dari sumbu y. Untuk menghitung komponen vektor untuk vektor F1 adalah pertama, kita harus mengetahui letak sisi OB dan AB. Ini dapat dilakukan dengan cara mencari letak sudut siku-siku dan letak sudut α. Sudut siku-siku selalu berada di sebrang sudut α. Sudut α dalam vektor F1 ini adalah sudut 30o.
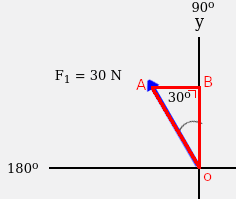
Setelah diketahui letak sisi OB dan AB, dapat diketahui untuk menghitung komponen vektor y dapat digunakan rumus sisi OB, sedangkan untuk menghitung komponen vektor x dapat digunakan rumus sisi AB. Ini karena sisi OB pada vektor F1 menghadap secara vertikal dan sisi AB menghadap secara horizontal. Berikut perhitungan komponen vektor x dan y untuk vektor F1.
- F1x = AB = F × sin α = 30 × sin 30 = 15
- F1y = OB = F × cos α = 30 × cos 30 = 26
-
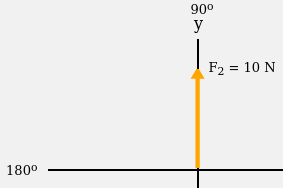
Untuk vektor F2, diketahui memiliki panjang 10 N dan menghadap ke utara atau sumbu y positif. Rumus yang digunakan untuk menghitung komponen vektor ini sama seperti vektor F1 karena letak segitiga siku-sikunya sama seperti vektor F1, hanya saja sudut α-nya adalah 0. Perhitungan komponen vektor untuk vektor F2 adalah :
- F2x = AB = F × sin α = 10 × sin 0 = 0
- F2y = OB = F × cos α = 10 × cos 0 = 10
-
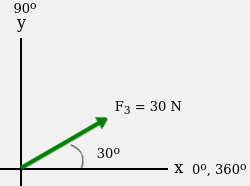
Untuk vektor F3, diketahui memiliki panjang 30 N dan menghadap 30o dari sumbu x. Maka letak segitiga siku-sikunya adalah sebagai berikut:
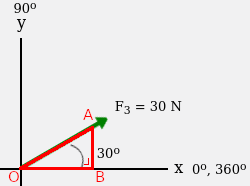
Sehingga perhitungan komponen vektor x dan y untuk vektor F3 adalah :
- F3x = OB = F × cos α = 30 × cos 30 = 26
- F3y = AB = F × sin α = 30 × sin 30 = 15
-
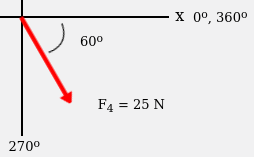
Untuk vektor F4, diketahui memiliki panjang 25 N dan menghadap 60o dari sumbu x. Maka letak segitiga siku-sikunya adalah sebagai berikut:
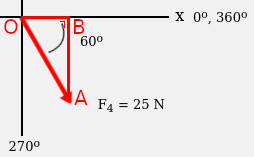
Sehingga perhitungan komponen vektor x dan y untuk vektor F4 adalah :
- F4x = OB = F × cos α = 25 × cos 60 = 12.5
- F4y = AB = F × sin α = 25 × sin 60 = 22
Setelah semua komponen vektor diketahui, selanjutnya kita perlu menentukan apakah setiap komponen vektor x dan y yang sudah kita hitung tersebut adalah bertanda negatif atau positif.
| Bertanda positif jika | Bertanda negatif jika | |
|---|---|---|
| Komponen vektor x | Vektor berada di bagian kanan | Vektor berada di bagian kiri |
| Komponen vektor y | Vektor berada di bagaian atas | Vektor berada di bagian bawah |
Untuk contoh soal kita, maka hasilnya akan menjadi seperti ini :

- Vektor F1 berada di bagian kiri sumbu x dan di bagian atas sumbu y, maka komponen vektornya menjadi seperti berikut:
- F1x = -15
- F1y = 26
- Vektor F2 berada di tengah sumbu x dan di atas sumbu y. Jika vektor berada di tengah sumbu, maka anggap saja tandanya menjadi positif. Maka komponen vektornya menjadi seperti berikut:
- F2x = 0
- F2y = 10
- Vektor F3 berada di bagian kanan sumbu x dan di bagaian atas sumbu y, maka komponen vektornya menjadi seperti berikut:
- F3x = 26
- F3y = 15
- Vektor F4 berada di bagian kanan sumbu x dan di bagaian bawah sumbu y, maka komponen vektornya menjadi seperti berikut:
- F4x = 12.5
- F4y = -22
Setelah menentukan tanda positif atau negatif untuk semua komponen vektor, selanjutnya kita hitung resultan vektor x. Caranya sangat mudah, cukup tambahkan semua komponen vektor x untuk semua vektor. Maka resultan vektor x untuk contoh soal kita adalah :
- ΣFx = F1x + F2x + F3x + F4x = -15 + 0 + 26 + 12.5 = 23.5
Selanjutnya, kita hitung resultan vektor y. Caranya sama dengan cara menghitung resultan vektor x. Maka resultan vektor y untuk contoh soal kita adalah :
- ΣFy = F1y + F2y + F3y + F4y = 26 + 10 + 15 – 22 = 29
Terakhir, kita bisa hitung resultan vektor untuk semua vektor. Rumus untuk menghitung resultan vektor adalah :
| Rumus Resultan Vektor |
|---|
| R =√ (ΣFx)2 + (ΣFy)2 |
Maka resultan vektor untuk contoh soal kita adalah:
R =√ (ΣFx)2 + (ΣFy)2 =√ (23.5)2 + (29)2 = 38